
K를 몇개 사용해야 될까요? 어떤 거리를 골라야할까요?
슬프게도 K의 개수와 거리는 인공지능이 학습하면서 우리에게 알아서 알려주지 않는다.
인간이 학습전에 골라주어야 한다!
우리는 이걸 하이퍼 파라미터라고 부른다.

하이퍼 파라미터는 모델링할 때 사용자가 직접 세팅해주는 값이다.
우리는
+) 인공지능이 정해주는 값은 파라미터라고 부른다.
파라미터는 한국어로 매개변수이다.
파라미터는 모델 내부에서 결정되는 변수이다.
또한 그 값은 데이터로부터 결정됩니다.
사용자에 의해 조정되지 않는다.
하이퍼 파라미터는 어떻게 고를까? 3가지중 하나만 정답이다.
1. 학습이 제일 잘 되는 하이퍼파라미터 고르자!
2. 학습을 하고 시험을 봐서 시험 결과가 제일 좋은 하이퍼 파라미터를 고르자!
3. 학습을 하고 검증을 하여 검증 결과가 제일 좋은 하이퍼 파라미터를 고르고 이를
시험을 활용하여 최종 결과를 보고 제출하자!
당연하게도 말이 제일 긴 3번이 옳다.

1이 안되는 이유: K = 1일 때 제일 잘 적용된다고 한다.
그리고 훈련 데이터에만 최적화 되어있는 매개변수를 고르면? 오버피팅이 난다.

2가 안되는 경우
우리는 훈련데이터를 통해 보이지 않는 (감이 가장 무서운 법) 데이터를 맞춰야 한다.
시험 데이터가 보이지 않은 데이터 역할을 하는 건데 얘를 모델끼리 비교하는데 쓴다면
시험 데이터는 정답까지 공개가 되었으니 보이지 않은 데이터의 역할을 잃어버리게 된다.
고3의 시점에서 생각한다면 수능 시험이 유출된 셈이다.
기계학습의 문제에 나온 것인데 학습데이터가 부족할 때, 시험데이터를 보고 파라미터를 고쳐도 될까?
절대 안된다. 나는 이걸 가능하다고 생각하여 O를 찍었고 그 결과 틀렸다.
+ 모델이 시험데이터를 보고 시험데이터에 맞게 가중치(파라미터)나 bias를 업데이트 한다고 한다.

훈련을 한 다음, 중간에 검증을 꼭! 하여 검증 결과중 제일 좋은 방안을 고른다!
학습 데이터와 검증 데이터의 차이:
학습 데이터는 컴퓨터가 정답을 볼 수 있다.
검증데이터: 우리는 답을 볼 수 없지만 컴퓨터는 직접적으로 답을 볼 수 없다.
좋은 하이퍼 파라미터를 선택하고 학습을 끝까지 시킨 후,
모든 준비를 한다음 시험 데이터를 보고 그 상태 '그대로' 제출을 하면 된다.

그외) Cross Validation이 있다.
5개의 fold를 나눌 때 1에서 4까지의 작은 fold에는 학습을 수행한다. 그리고 마지막 fold는 검증을 하는 방식.
이걸 5번 반복하여 제일 좋은 모델을 고른다.
이거 딥러닝에서는 너무 비싸고 시간이 오래 걸려서 불가능하다!

여기서 쓰는 데이터는 CIFAR 10이다.
저거 싸이퍼 10인 줄 알았는데 씨파10이라고 읽는다.
FeiFei Li라는 전설적인 비전 관련 교수가 이미지와 라벨링을 하나씩 하여 만든 대형 데이터 셋이다.
10개의 카테고리를 분류하기 때문에 뒤의 숫자가 10이다. (100개의 카테고리 분류는CIFA100이다.)
사진과 사진에 해당하는 라벨로 되어있다. (라벨은 숫자로 나온다.)
이 데이터를 KNN알고리즘을 이용해 하나씩 분류를 할 예정이다.

하이퍼 파라미터들을 여러번 수행 한 결과 K가 7부근에서 잘 작동하는 것을 발견

이렇게 분류를 하였다. 마음에 드는가? 뭔가 잘맞춘거 같기는 한데 자세히 보면 어딘가 이상하다는 점을 눈치 챌 수 있다. 비슷한 자세를 취하면 같은 종으로 분류하는 역효과가 있다! 눈사람을 만들고 거기다가 돌맹이 3개를 박는다면
아마 하얀색 강아지로 분류될 것이다.

KNN알고리즘은 비전에 쓰일 수 있을까? 절대 없다.
3가지 이유를 들어서 그 이유를 말할 수 있다.
1. 픽셀간의 거리가 정보가 없다. 그냥 단순 거리이다.
원본 사진이 있고 이사진을 3가지 방식으로 바꾸어 보았다.
- 눈 입 가리기
- 1픽셀만 바꾸기
- 사진의 색조를 바꾸기
이러고 원본 사진과 비교를 하였을 때 세사진과 원본사진의 거리가 모두!! 같았다.
2. 시험 볼때 너무 오래걸린다. 학습시간이 오래걸리고 시험시간이 적어야 되는데 이는 대참사이다.
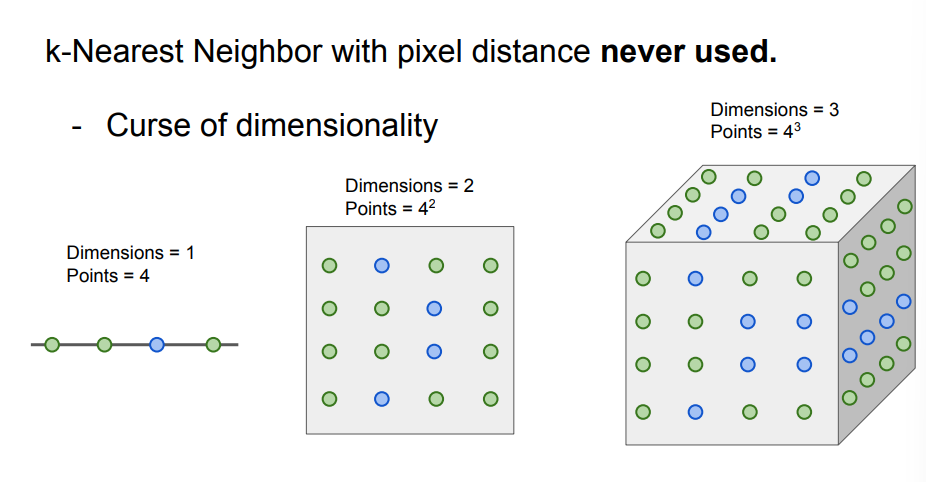
3. 차원의 저주가 존재한다.
n개의 데이터를 분류할 때 데이터가 x차원을 가진다면, 학습 데이터의 개수가 n의 x제곱 정도있어야
오버피팅 없이 잘 분리가 가능하다는 저주이다.
예를 들어 구별해야 되는 데이터는 4개이고 차원이 1이면
4의 1제곱하여 4개의 학습데이터가 필요하다.
2차원이면 4의 2제곱인 16개의 학습데이터가 필요하며
3차원이면 4의 3제곱을 하여 64개의 데이터가 필요하다!
픽셀값이 0부터 255까지 가지니까 256차원인데
구별해야되는 데이터의 256제곱을 하라니... 너무 끔찍하다.
KNN이 망해서 인공지능이 끝났을까? 아니다.


선형 분류기가 등장하였다.
개요)입력 이미지가 주어지면 W라는 가중치(파라미터)와
선형 연산을 하여 출력값을 뱉는 방식이다.

이미지를 완전히 펼친 다음, 가중치와 서로 곱한다음 bias를 더하여 최종 값을 뱉는 방식이다.
그런데 사진이 어떻게 파라미터와 연산을 할 수 있을까?
컴퓨터에서는 이 사진을 벡터로 취급한다.
벡터와 가중치를 가진 벡터끼리 서로 곱한다고 생각하면 된다.

입력사진이란 벡터와 가중치란 벡터끼리 서로 유사성을 보기위해 내적을 한다고 생각하면 된다.
만약 입력사진을 가중치에 넣었는데 양수이면? 입력사진과 가중치가 서로 유사하다.(같은 방향을 가진 예각 벡터이다.)
만약에 음수면? 서로 많이 다르다.(다른 방향을 가진 둔각 벡터이다.)
0은 잘 안나오는 경우라서 제외하였다.
서로 벡터 곱을 한다음 b를 더하는데 b는 bias로 편향을 의미한다.

구체적인 예시) 고양이가 픽셀이 4개이고 구별해야 되는 카테고리의 개수가 3개여서 3행 4열의 가중치 벡터가 있다고
가정하자. (가중치는 카테고리의 개수 * 입력 사진의 픽셀개수)로 이루어져 있다.
고양이 사진의 픽셀이4개인데 이 4개를 1줄로 풀어버린다.(이걸 평탄화라고 한다.)
그다음 W와 서로 행렬곱을 수행한다.
이 연산이 끝나면 bias를 더하여 최종 값을 구한다.
참고로 고양이가 음수이고 개의 값이 가장 큰 걸 보아 학습이 잘못 되었다.
나중에 학습이 끝나고 W를 보면 W는 구별해야 하는 class의 견본을 가지고 있다고 한다.

인공 신경망이 생각하는 견본이다.
비행기: 파란 무언가, 자동차: 보라색의 몸과 파란색이 합쳐짐(자동차가 이렇게만 생기지 않은 걸 모두가 안다.)
말: 머리가 머리가 2개처럼 보임.
이렇든 1개의 층으로 모든 사진을 구별하고자 하였더니 문제가 생기는 것을 알 수 있었다.
선형 분류기는 각 class 별 견본을 1개 밖에 출력하지 못한다.
그래서 학습 데이터들을 통합해서 평균적인 모습 한 개를 수렴해서 내보낸다.
모델이 복잡해질수록 한 가지 견본에만 집중하지 않게 된다. (견본이 다양해진다.)
여러층으로 쌓으면 다양한 견본을 얻게 된다.

선형 분류는 데이터가 존재할 때 데이터에 선을 그어서 분류를 하는 것이라고 생각하면 된다.
여기까지 나온 것은 1층의 선형 분류기이다.
1층의 선형 분류기에는 여러 한계가 존재한다.

위의 3가지 사례를 살펴보면 1개의 선으로 빨강과 파랑을 분리하는 것이 불가능하다는 것을 알 수 있다.
다음에는 이를 해결하고자, 여러개의 선형 분류기층에대해 다룰 예정이다.
'인공지능 관련 강의' 카테고리의 다른 글
| 패스트캠퍼스 온라인 강의 수강후기 (0) | 2023.12.15 |
|---|---|
| 무작정 쓴 CS231n 2강 (1) (0) | 2022.03.01 |

